Mouvement circulaire uniforme et sinusoïde
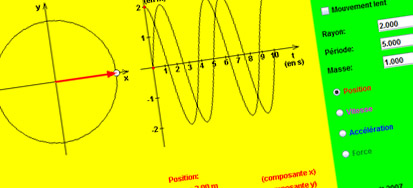
• Cette animation montre comment l’abscisse et l’ordonnée d’un point soumis à un mouvement circulaire uniforme sont des fonctions sinusoïdales (page 22 de TLM1). Possibilité de faire varier la vitesse angulaire (pulsation), et donc la période.
• Permet de visualiser le déplacement d’un point M et de la base associée lorsqu’on fait varier ses coordonnées cylindriques (page 59 de TLM1).
• Permet de visualiser le déplacement d’un point M et de la base associée lorsqu’on fait varier ses coordonnées sphériques (page 59 de TLM1).
Trajectoire parabolique d’un projectile
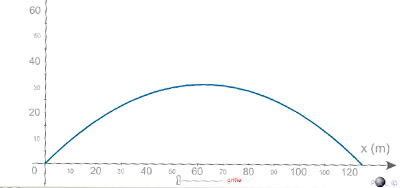
• Cette animation permet de visualiser la trajectoire d’un projectile, avec la possibilité de faire varier la vitesse initiale. Cette trajectoire est une parabole (page 82 de TLM1).
{Module 2 : Courbes et graphiques}
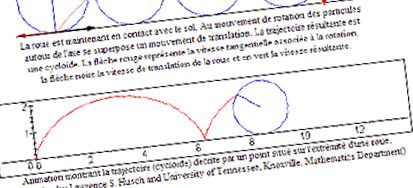
• Cette animation présente la cycloïde, trajectoire d’un point d’un cercle roulant sans glisser sur une droite horizontale (page 169 de TLM1)
L’ellipse obtenue par déformation du cercle
• Cette animation montre la génération d’une ellipse comme image d’un cercle par l’affinité d’axe Ox de rapport 0,5. Cliquer sur l’écran pour démarrer l’animation (page 178 de TLM1).
Construction de l’ellipse par la propriété bifocale
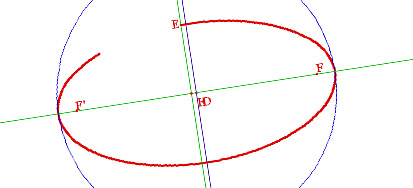
• Cette animation présente “l’ovale des jardiniers”. On peut faire varier l’excentricité de 0 à (presque) 1 et voir ainsi comment l’ellipse s’aplatit lorsque l’excentricité augmente, tandis que les foyers s’éloignent du centre (page 180 de TLM1).
{Module 3 : Calcul différentiel et intégral}
Oscillations libres d’un ressort
• Elles sont régies par une équation différentielle linéaire homogène du second ordre à coefficients constants. La différence entre phénomènes apériodiques et pseudo-périodiques s’observe facilement car on peut faire varier les paramètres (page 232 de TLM1).
Effondrement du pont de Tacoma (phénomène de résonance)
• Cette vidéo montre l’effondrement du pont de Tacoma (USA) en 1940, à la suite de phénomènes de résonance provoqués par des vents violents. Les phénomènes de résonance sont régis par une équation différentielle linéaire du second ordre à coefficients constants avec un second membre sinusoïdal (page 239 de TLM1).